ADKG
Estimated time to read: 4 minutes
Asynchronous Distributed Key Generation (ADKG) is a building block for any decentralized protocol that allows a set of mutually non-trusting nodes to jointly generate a public/private key pair.
This key pair is used to bootstrap the cryptography subsystems without a trusted third party.
Arcana Network ADKG implementation is used for non-custodial key pair generation and onboard the SDK users to sign blockchain transactions. None of the individual ADKG nodes have access to the user’s key ensuring security and robustness of the system.
At Arcana, have come a long way since the Arcana Auth SDK alpha release that offered a distributed key generation feature (DKG).
Several shortcomings in the earlier DKG regarding trusted dealer, robustness have been resolved in the state-of-the-art asynchronous distributed key generation (ADKG) protocol built into the Arcana key generation subsystem. We have collaborated with some of the leading cryptography experts and researchers to fold recent advances in asynchronous DKG technology in Arcana Auth SDK. Refer to the Arcana Technical Whitepaper for more details on ADKG.
Why is ADKG better?
Earlier, the Arcana Network protocol used DKG with a trusted dealer mechanism which had its shortcomings such as:
- Dealer has access to all keys as they are the ones generating the keys.
- Regeneration of lost shares by a node going down or exiting the network was not automated
The new ADKG implementation is more robust than Arcana Network’s previous DKG implementation as it does not involve any trusted dealer or a third party.
Also, unlike the other synchronous DKG protocol models, ADKG protocol is immune to any underlying synchronous network assumptions. By asynchronous network, we mean a network where the presence of a malicious adversary can corrupt a threshold of nodes and delay message sharing but must eventually deliver all messages sent between honest nodes.
Assumptions
The ADKG protocol works under the assumption that in an asynchronous network of n ≥ 3t + 1 nodes, where at most t nodes could be malicious.
The protocol can achieve an expected communication cost of O(κn\(^3\) ) and terminates in expected O(log n) rounds. Here κ is the security parameter. For example, if a collision-resistant hash function is used, in that case, κ denotes the size of the hash function's output.
How does ADKG work?
ADKG requires a set of at least 4 connected nodes at a minimum for accommodating a maximum of 1 malicious node.
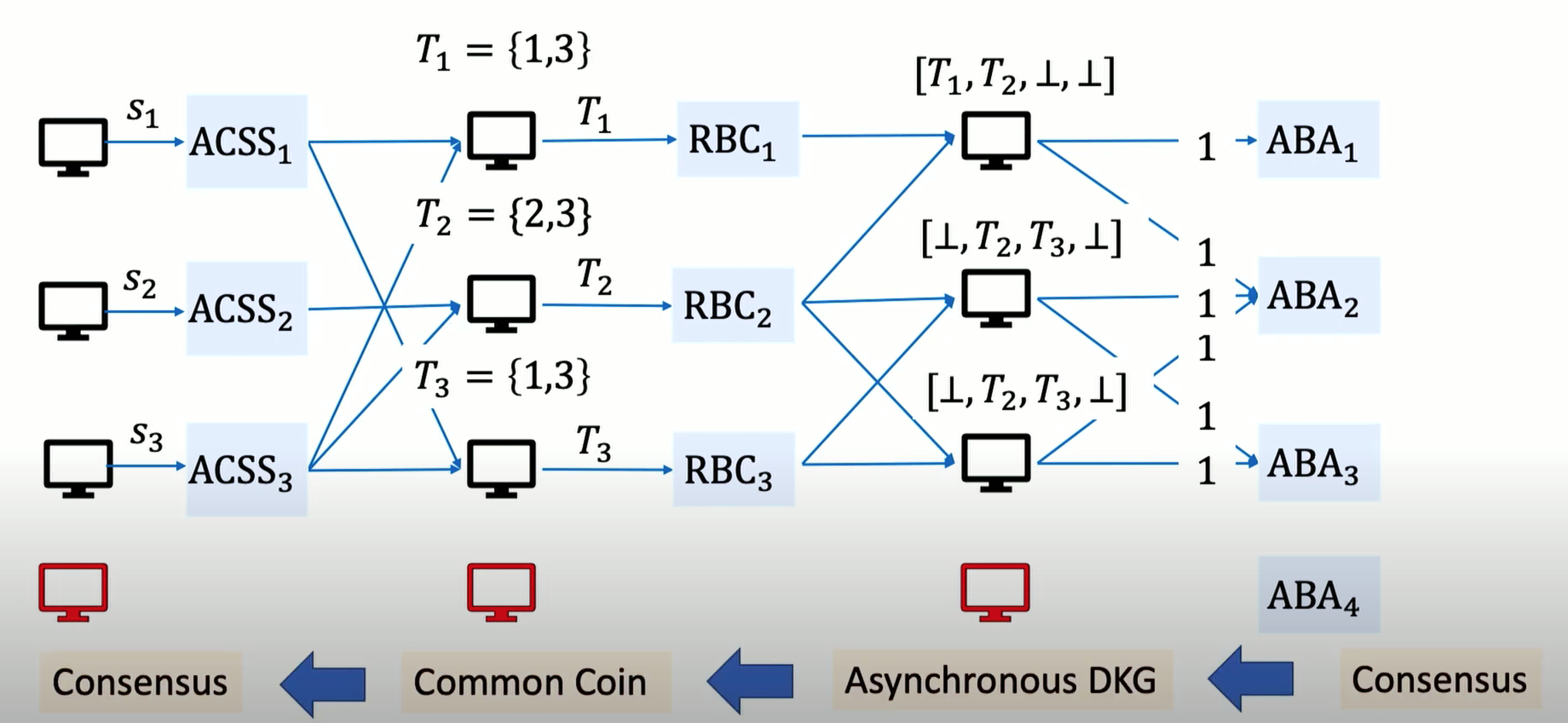
At a very high level, the protocol requires each node to independently generate secrets and then share a part of that secret with the other nodes. Each node then shares a proposed set of key shares with other nodes. Asynchronous Binary Agreement (ABA) voting is done by the nodes for each proposed set. Only the accepted and agreed-upon set is used to derive the key shares and then those key shares are combined to arrive at the final key pair. None of the nodes have full access to the secret key.
Let’s take a closer look at each of these 4 key phases in the ADKG protocol:
- Asynchronous Complete Secret Sharing (ACSS)
- Keyset Proposal Broadcast Phase
- Asynchronous Binary Agreement (ABA)
- Key Derivation Phase
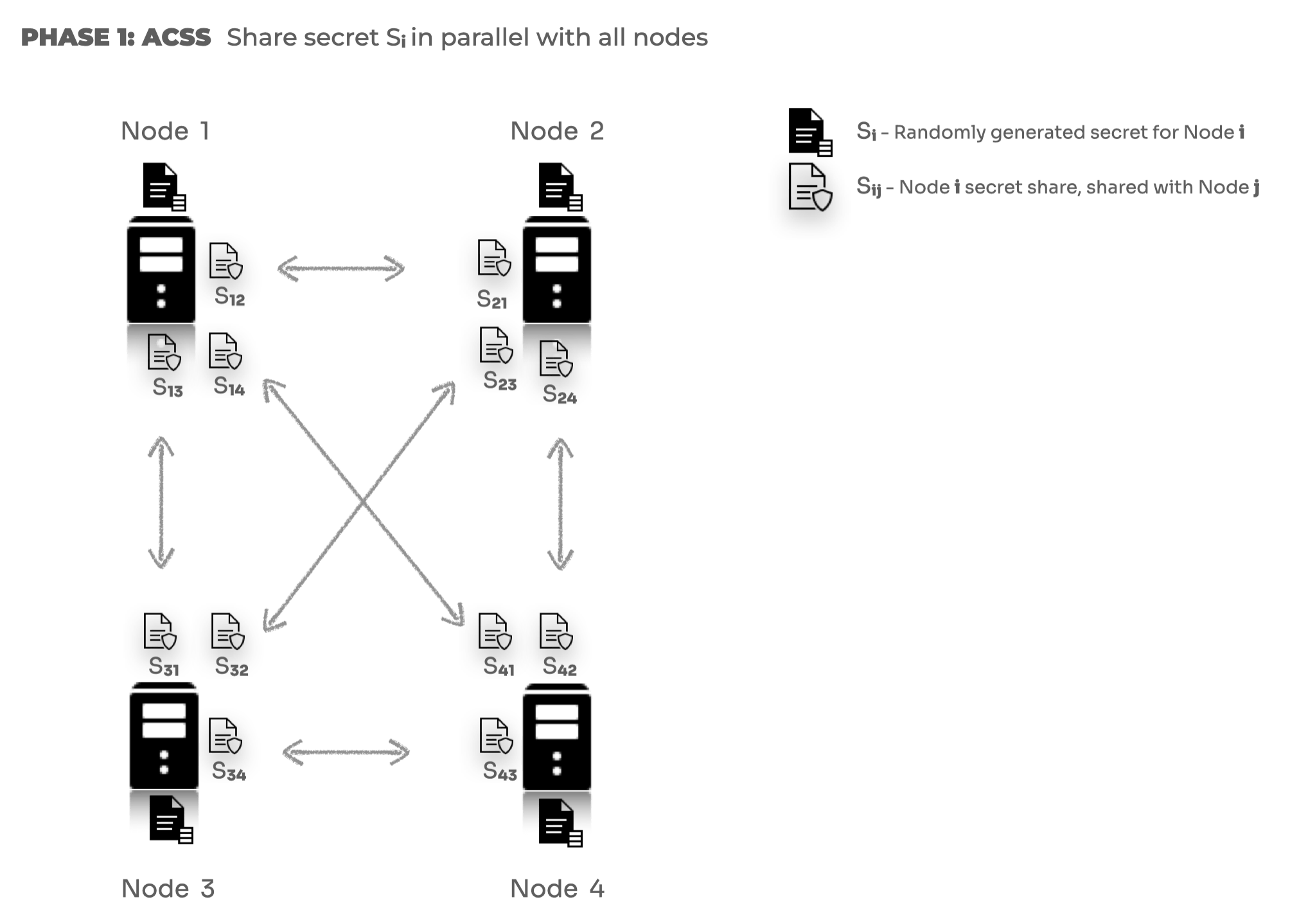
1. Asynchronous Complete Secret Sharing (ACSS)
The first phase is where each of the participating nodes generates its secret key shares independently and shares the selected key shares with the other nodes.
- Each participating node generates a secret.
- Every node splits the secret into n parts where n is the number of participating nodes.
- Each node shares the split secret key shares with other nodes in parallel.
At the end of the ACSS phase, each node has a set T of share index from all other participating honest nodes.
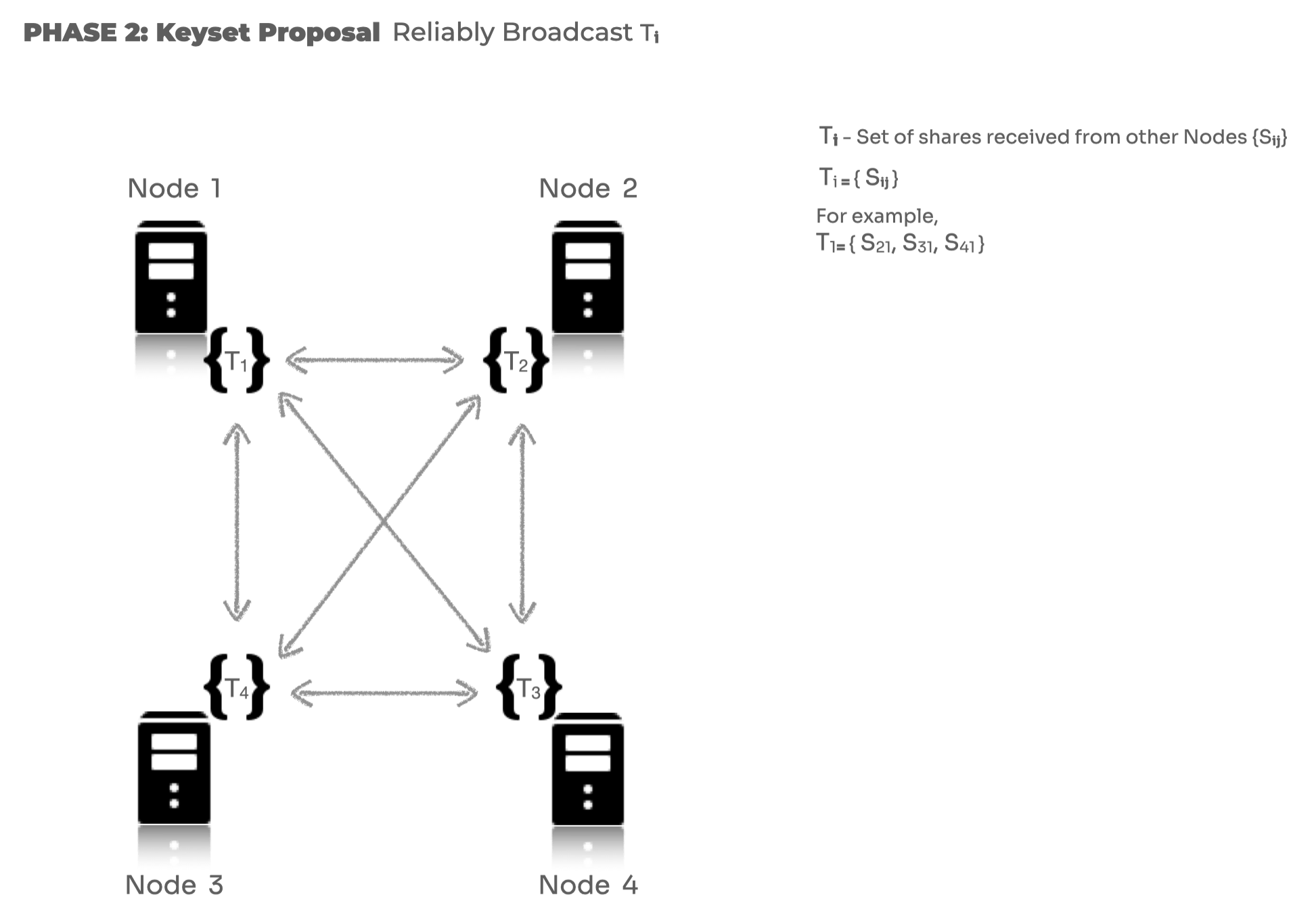
2. Keyset Proposal Broadcast
After the first phase, once each node has generated and shared key shares, each node has a set of key shares received from the other nodes. The index set of this set is shared with all the other nodes. Each node \(i\) reliably broadcasts its complete set \(T_i\) of share index that it collected in the previous ACSS phase.
At the end of this phase, each node has n T sets containing share index from all the other participating nodes.
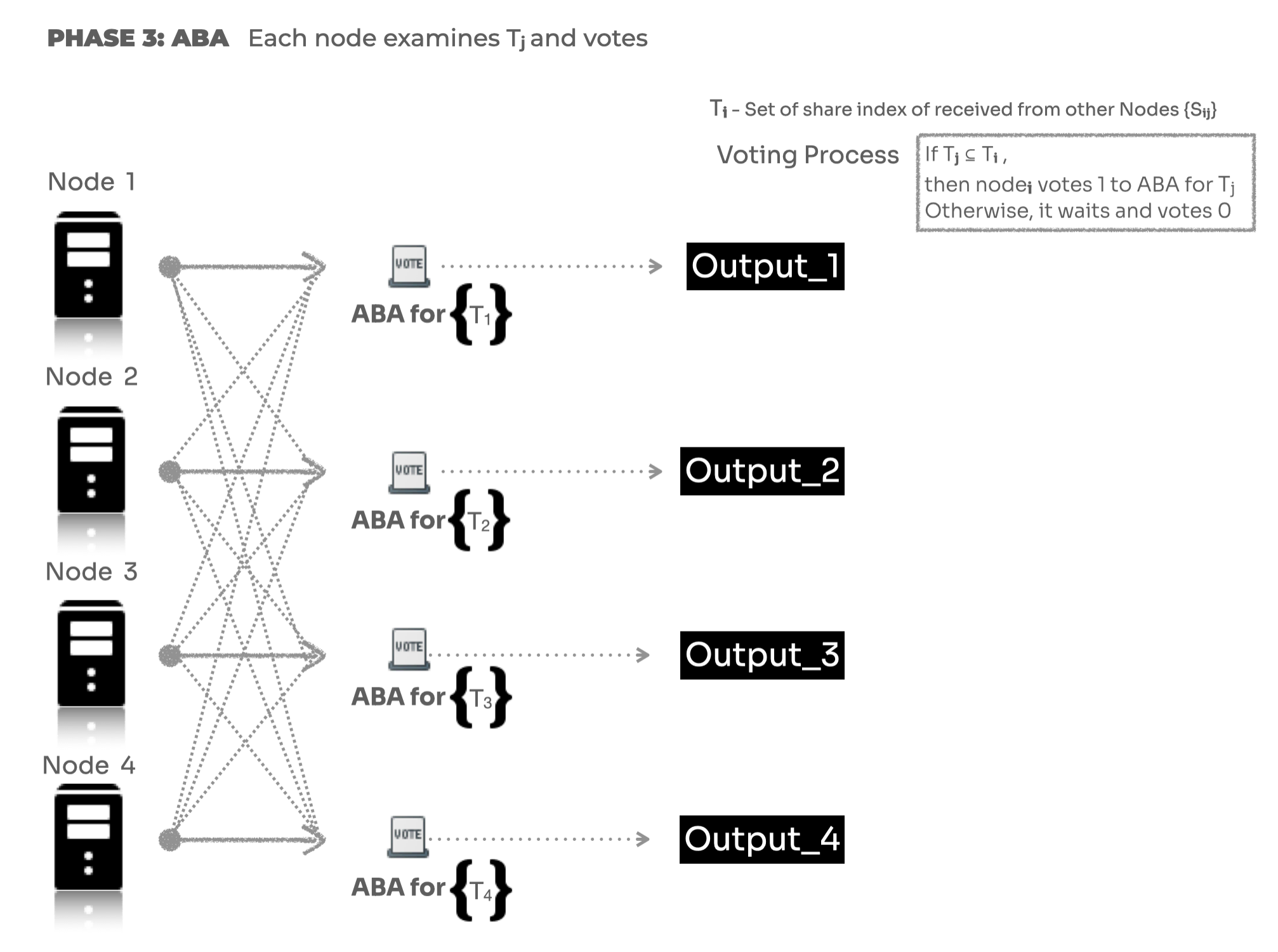
3. Asynchronous Binary Agreement
In this phase, each node has the T sets or the proposed share set from the other nodes and is required to vote.
- During the agreement phase, nodes try to agree on a subset of valid key set proposals.
- Every node looks at its own and other nodes’ T set received in the previous phase and if the T set is a subset of its own T set or equal set then it votes a 1 for it to the ABA.
At the end of this phase, votes from all nodes are generated for every proposal set T submitted by each participating node.
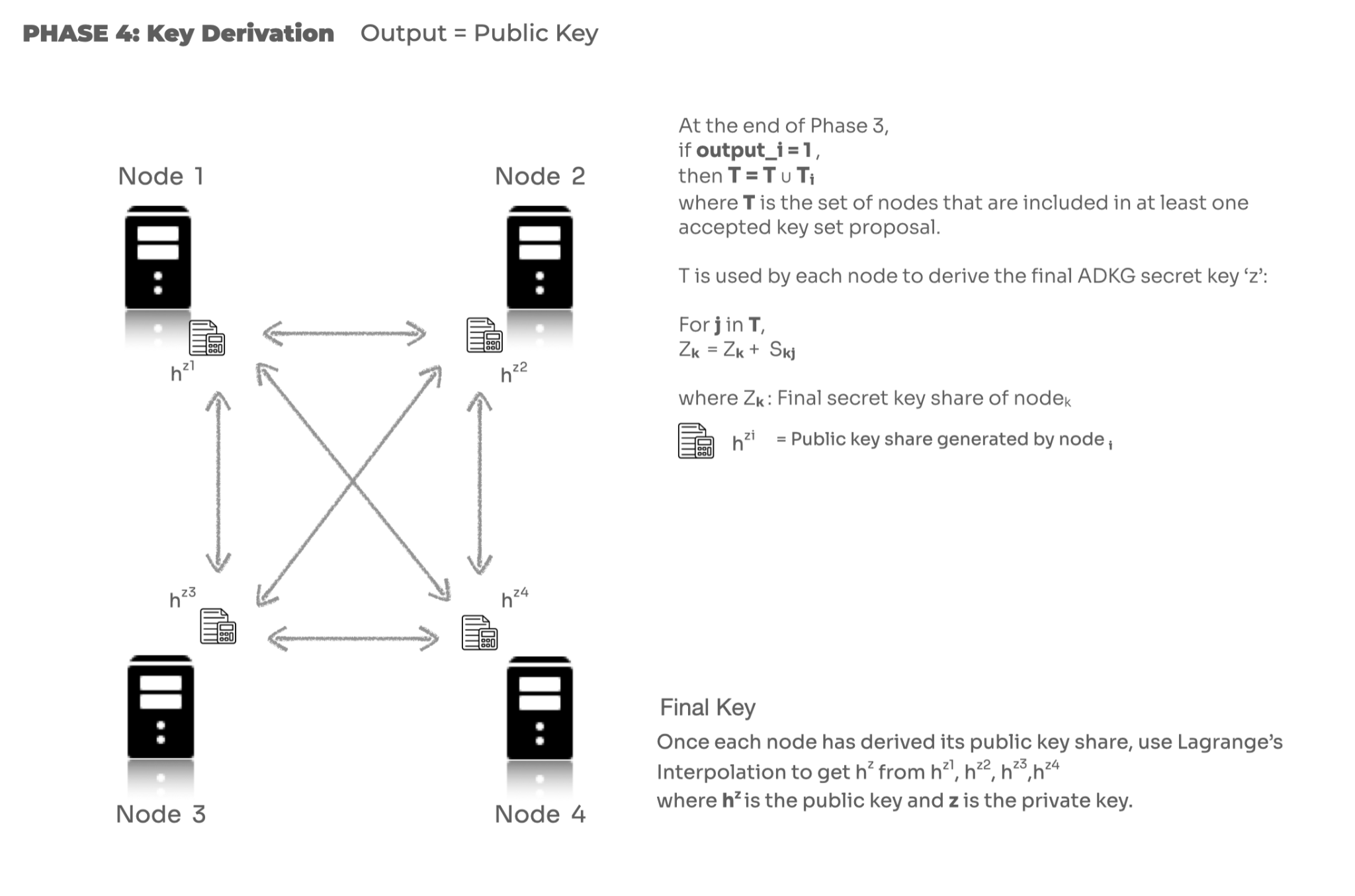
4. Key Derivation
During this phase, the union of elements in key set proposals is used to derive the final secret key share for each node.
- If the ABA terminates with an output of 1, that means the key set proposal is accepted.
- Each node uses the union of all accepted key set proposals to generate its own secret key share. What this means is that if node j was in the final accepted proposal union set, node k will generate its final share by including or adding the share given by node j to node k during the ACSS phase. In short, if T = T ∪ T\(_i\), then for j in T, \(Z_i=Z_i+S_{ij}\) where Z\(_i:\) Final share of node\(_i\)
- After sharing terminates, each node derives its share of the public key, \(h^{z_i}\) where \(i\) is the node number, using Lagrange’s interpolation.
- Each node then shares its public key share with all the other participating nodes.
At the end of this phase, h\(^z\) is derived from \(h^{z_1}\),...,\(h^{z_4}\) at all nodes. Using these public key shares from the threshold number of participating nodes, each node can generate the final agreed-upon public key.
The secret key is not accessible to any single node. Each node only has its share of secret key information.
For more information, refer to the Arcana Technical Whitepaper.